'If you're going to have a mental breakdown the best place to have it is in Spring and in Cambridge.' These are the words of artist, visionary and outsider architect John Devlin, whose book 'Nova Cantabrigiensis' presents his intriguing vision of a utopian island based on Cambridge, which he considers the ideal city.
Originally from Halifax, Nova Scotia, Devlin came to Britain in 1979, studying Theology at St Edmund's College, Cambridge, and falling in love with the city's architecture and atmosphere. When mental illness forced him to cut short his studies and return home to Canada - abandoning his ambition to enter the priesthood - he became obsessed with discovering the secret to 'the Cambridge essence'.
To aid his recovery, he imagined an idyllic island where he would be as happy as he had been in Cambridge. Over the next ten years, he created over 360 illustrations - dream-like sketches of redesigned collegiate-style buildings on an imaginary island that he situated in the Minas Basin, Nova Scotia. Devlin's designs often incorporate elements borrowed from several existing buildings, as well as fantastical additions such as lasers and a carousel in King's Court.
Twenty-two of these fascinating sketches were exhibited at King's Art Centre at the University of Cambridge last year and resulted in the publication of Nova Cantabrigiensis (literally meaning New Cambridge in Latin). The book contains a selection of his illustrations as well as a brief outline of his mathematical theories about architecture.
Devlin, who studied architecture before deciding to become a priest, was fascinated by the harmonious juxtaposition of Gothic and Classic styles in King's College Chapel and the adjacent Gibbs' building, distilling their relationship into a semi-mathematical equation which he calls 'The King's Constant' - based on the ratio of the volumes of the two buildings.
Devlin suggests using this equation and exporting it, re-creating the genius loci of Cambridge elsewhere. 'My theory,' he says, 'is that for ideal design, there is an Ideal Ratio. I have been hunting for such a constant which would, if found, make design scientific. After many false starts, I am presently cautiously concluding that this ratio is 5:10:1.'
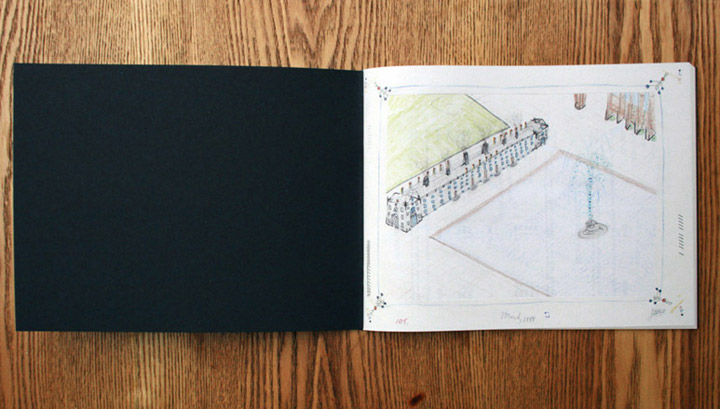
Illustration ’March, 1988’ from Nova Cantabrigiensis
Devlin’s Nova Cantabrigiensis presents his vision of a utopian city based on Cambridge
Illustration ’March, 1988’
Illustration ’8 Jan, 1989’
The book includes an explanatory text based on Devlin’s writings, outlining his mathematical theories concerning architecture
-
An Indian mud house - and more, on Sketch Design Studio's natural material wondersSketch Design Studio in Rajasthan, India does wonders with the simplest ingredients
-
Experience this Singapore apartment’s Zen-like qualities and cocooning urban havenWelcome to Singapore apartment The Rasidence, a spacious, Zen-like interior by Right Angle Studio
-
The Park: step inside Jeremy King's mid-century dinerOne of several 2024 openings from restauranteur, Jeremy King, food critic Ben McCormack books in at The Park
-
'Tropicality' explored in Indonesian architect Andra Matin’s first monograph'Tropicality' is a key theme in a new book on Indonesian architect Andra Matin, whose work blends landscape, architecture and living
-
‘A Time ⋅ A Place’ is a lovingly compiled photographic portrait of cars and architecture‘A Time ⋅ A Place’ is a celebration of the European Car of the Year and changing perceptions of modern design, pairing the best buildings of the age with their automotive contemporaries
-
Álvaro Siza’s new monograph through the lens of Duccio Malagamba is impactful and immersiveÁlvaro Siza and photographer Duccio Malagamba collaborate on a new monograph by Phaidon; ‘Before / After: Álvaro Siza Duccio Malagamba’ celebrates the Portuguese architect's work
-
Marcio Kogan’s Studio MK27 celebrated in this new monograph from Rizzoli‘The Architecture of Studio MK27. Lights, camera, action’ is a richly illustrated journey through the evolution of this famed Brazilian architecture studio
-
‘Interior sculptor’ Christophe Gevers’ oeuvre is celebrated in new book‘Christophe Gevers’ is a sleek monograph dedicated to the Belgian's life work as an interior architect, designer, sculptor and inventor, with unseen photography by Jean-Pierre Gabriel
-
Flick through ‘Brutal Wales’, a book celebrating concrete architecture‘Brutal Wales’ book zooms into a selection of concrete Welsh architecture treasures through the lens of photographer Simon Phipps
-
Architecture books to inspire shelf loveHere at Wallpaper*, we’ve got architecture books piling up; among them, these are the photographic tomes, architects’ monographs and limited editions that we couldn’t resist
-
Pioneering modernist Henry Kulka's life and career tracked in limited-edition monographCzech-New Zealand architect Henry Kulka, a man who spread modernist ideals half way around the world, is celebrated in Giles Reid and Mary Gaudin’s richly illustrated monograph
